${}$ 最近、パタヘネの第５版を読んでいます！
結構ボリュームはあるのですが、なんとか第５章まで読みました。
名著と謳われているように、ページを進めるほどにコンピュータの奥深さが身にしみます。
もっと早く読めばよかったなぁ。昔の自分は何をやっていたんだ！？
（ブログを読み返す）
そっか、Bilateral Solverをやっていたのか。

・・・一応、Bilateral Solverについて説明します。
Bilateral Solverとは、Googleの研究者が発表した画像処理用の高速ソルバです。
かつて僕は論文を読みながら、C++による実装に取り組んでいました。
僕はこれまでBilateral Solverを知っている人に会ったことはないですw

そうそう、パタヘネの話でしたね。
記憶階層について読んでいると、Bilateral Solver実装時の疑問を、ふと思い出しました。
「行列の転置って処理速度遅いよな・・・」
Bilateral Solverでは10万x10万サイズの行列を扱います。
最終的な解を求めるまでに様々な計算をするのですが、
なぜか行列の転置にかかる時間がめちゃくちゃ長いのです！
ホント謎でした。
当時の僕は、コンピュータの中では不思議な現象が起きる、という結論に至ったのですが・・・

冷静に考えたら、そんな訳はありませんw
今思うと、あの時の現象はキャッシュミスが原因だったのかもしれません。
そうとなれば、さっそく調査だーーーー！

転置のパフォーマンス

最初に、不要とは思いますが、行列の転置とはどのような処理かを説明します。
転置前の行列があります。
\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}

転置後はこうなります。 \begin{pmatrix} 1 & 4 & 7\\ 2 & 5 & 8 \\ 3 & 6 & 9 \end{pmatrix}

それでは調査開始です！
本当に転置処理は遅いのか、以下の３パターンの速度を比較してみます。

行列Aの転置処理
行列Aと行列Bの加算
行列Aと行列Bの乗算

そんなの実行環境やプログラムの構造、行列のサイズに依るって？？
せやな！！！
今回は調査はあくまで一例ということで。

★使用するパソコンのスペック

Macbook Air（13-inch, Mid 2011）
CPU：1.7GHz Intel Core i5、32bit、Sandy Bridge?
一次キャッシュ：32kB
二次キャッシュ：256kB
三次キャッシュ：3MB
メモリ：4GB

いつの時代のスペックだよって感じですが、普段使いはこれで十分なんだからね！！

★Cプログラム

各処理の実行時間を図るプログラムはこんな感じにしました。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

void transposeMatrix(float **mat_a, int size)
{
    float tmp;
    for (int i = 0; i<size; i++)
        for (int j = i+1; j<size; j++) {
            tmp = mat_a[i][j];
            mat_a[i][j] = mat_a[j][i];
            mat_a[j][i] = tmp;
        }
}

void addMatrix(float **mat_a, float **mat_b, int size)
{
    for (int i = 0; i<size; i++)
        for (int j = 0; j<size; j++)
            mat_a[i][j] = mat_a[i][j] + mat_b[i][j];
}

void multiplyMatrix(float **mat_a, float **mat_b, int size)
{
    for (int i = 0; i<size; i++)
        for (int j = 0; j<size; j++)
            mat_a[i][j] = mat_a[i][j] * mat_b[i][j];
}

int main(int argc, char *argv[])
{
    int size = atoi(argv[1]);
    int mode = atoi(argv[2]);

    float **mat_a, **mat_b;
    int tmp = 0;
    mat_a = (float**)malloc(sizeof(float*) * size);
    for(int i = 0; i<size; i++)
        mat_a[i] = (float*)malloc(sizeof(float) * size);
    mat_b = (float**)malloc(sizeof(float*) * size);
    for(int i = 0; i<size; i++)
        mat_b[i] = (float*)malloc(sizeof(float) * size);


    clock_t start, end;
    double time;
    start = clock();
    switch (mode)
    {
        case 0:transposeMatrix(mat_a, size);
               break;
        case 1:addMatrix(mat_a, mat_b, size);
               break;
        case 2:multiplyMatrix(mat_a, mat_b, size);
               break;
    }
    end = clock();
    time = (double)(end - start)/CLOCKS_PER_SEC;
    printf("%0d %0.6f\n", size, time);
}

シェルの引数を利用して、行列のサイズを10～5000と変えながら、実行時間を計測してみます。
さて、結果は如何に！？
グラフにまとめたので、下にスクロールしてください。

f:id:yukirunrun:20200606234412p:plain
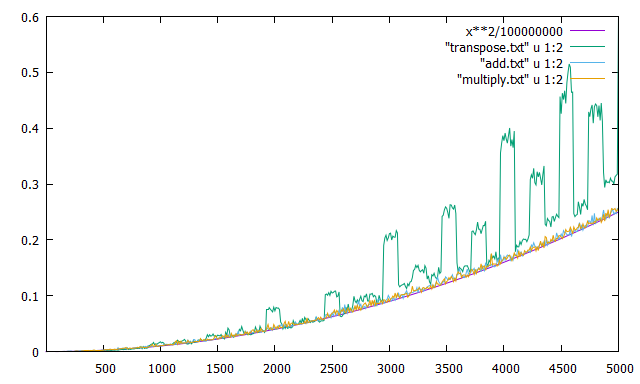
グラフの横軸は行列のサイズ、縦軸が所要時間です。
転置が緑色、加算が水色、乗算が橙色のグラフです。
参考までに、紫色はプログラムとは関係のない２乗曲線です。

グラフから明らかなように、転置処理が最も遅いという結果になりました！
やっぱり昔の記憶は間違っていませんでした。
よかった、よかった。

転置処理が遅い理由

そっかー、転置処理は遅いのかー
よくわかんないけど覚えておこっと。

・・・で終わると、昔の僕と変わりませんw

考察してみたいと思います。
パタヘネで記憶階層について学んだ僕は、この現象の原因をキャッシュミスであると推測しました。

キャッシュは、CPUがアクセス可能な記録素子のうち、特に応答時間が短い素子になります。
もしキャッシュに欲しいデータがある場合は、CPUのデータアクセス時間は短くなります。
もしキャッシュに欲しいデータがない場合は、CPUは代わりに、メインメモリやストレージまでデータを取りに行く必要があります。これはキャッシュミスと呼ばれ、CPUのデータアクセス時間は長くなります。取ってきたデータはキャッシュに格納され、次に同じデータにアクセスする際、アクセス時間は短くなります。
僕も詳しくないので、詳細はwikiや関連本を読んでください。

キャッシュによるアクセス時間短縮の効果は、データの時間的・空間的局所性に依存すると言われています。
その観点で、今回の３つの処理を見てみます。

★加算、乗算のプログラム f:id:yukirunrun:20200607005249p:plain

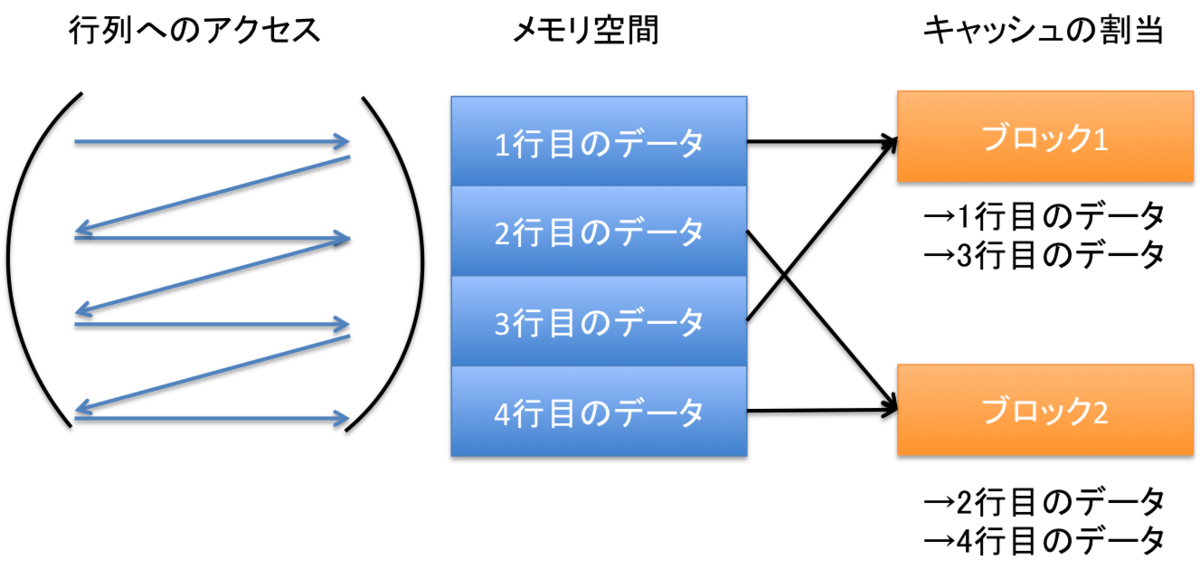
図のモデルはだいたいのイメージです。厳密なこと言いだすときりがないですが、大筋はあっていると信じています。
キャッシュの割当を以下のようにします。

ブロック１：１行目のデータまたは３行目のデータ
ブロック２：２行目のデータまたは４行目のデータ

加算、乗算プログラムは、メモリ空間に対して、上から順番にデータにアクセスしています。
キャッシュのデータの入れ替えは、

ブロック１：なし→１行目のデータ→３行目のデータ
ブロック２：なし→２行目のデータ→４行目のデータ

程度で済みます。
このプログラムは、データの時間的局所性、空間的局所性の両方に優れていると言えます。

★転置のプログラム f:id:yukirunrun:20200607005254p:plain

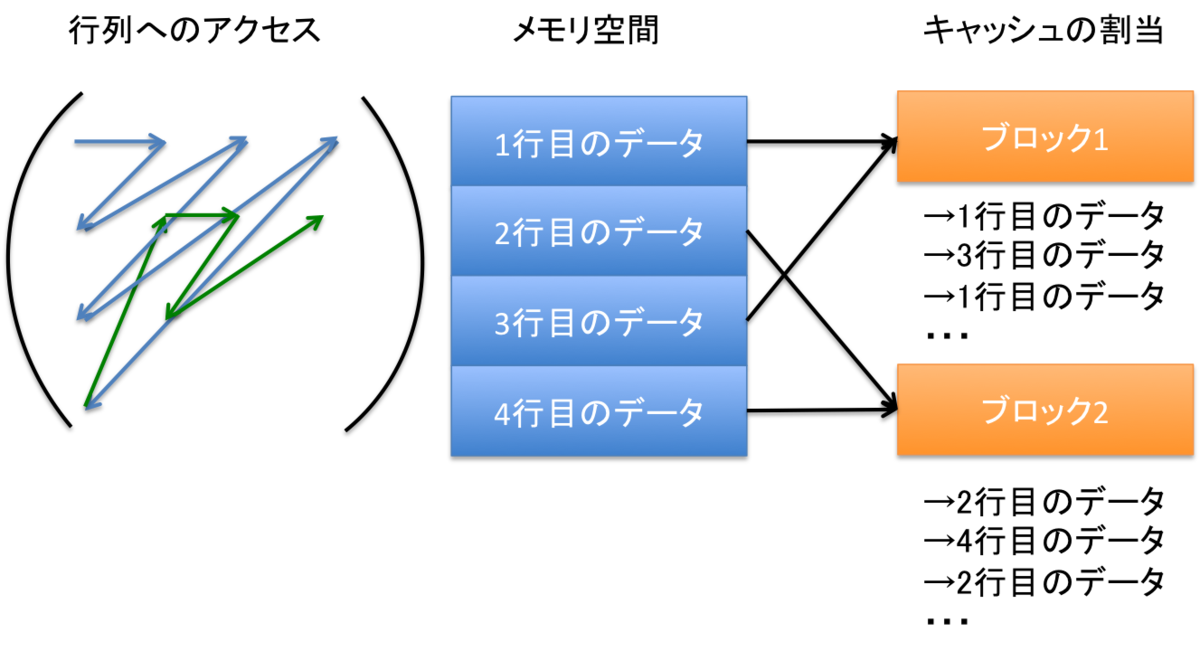
転置のプログラムは、メモリ空間に対して、ジグザグにデータにアクセスしています。
するとキャッシュのデータの入れ替えは、

ブロック１：なし→１行目のデータ→３行目のデータ→１行目のデータ→３行目のデータ→・・・
ブロック２：なし→２行目のデータ→４行目のデータ→２行目のデータ→４行目のデータ→・・・

のように何度も発生します。
このプログラムは、データの空間的局所性には優れていますが、時間的局所性には優れていません。

さて、もし上の説明が正しいと仮定するとだ。
キャッシュの容量が不足すると、プログラムの処理時間が遅くなるってことですよね。
実行環境の３次キャッシュの容量は3MByteです。
float型は4Byteなので、
$\sqrt[]{3 * 1024 * 1024 / 4} \simeq 887$
行列のサイズが約887x887を超えたあたりから、処理時間が悪化するはずです。
そのあたりのグラフを拡大してみます。

f:id:yukirunrun:20200607012249p:plain

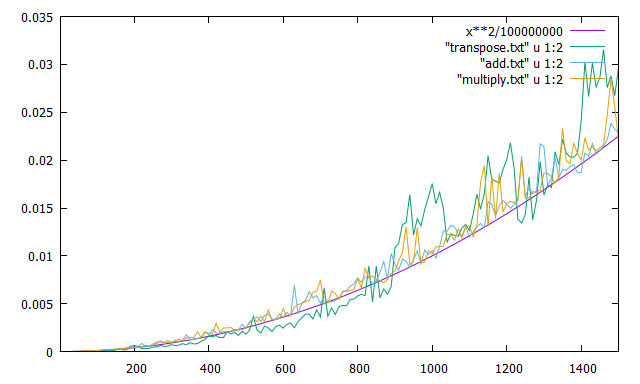
面白いぐらいに、800後半あたりからグラフが乱れているのがわかります。
キャッシュミスが原因である証拠ではないでしょうか！？

ついでにもう一つの謎にも触れておきます。全体のグラフをもう一度掲載します。

f:id:yukirunrun:20200606234412p:plain

転置のグラフは凸凹してますよね。
行列のサイズが増えると、処理時間は２乗オーダで増えてほしいのですが、なぜでしょうか？
何度もプログラムを実行しても、ほぼほぼ同じ結果になります。
偶然という可能性はなさそうです。

グラフを見ていると、行列のサイズが500増えるごとに似たようなパターンを繰り返しています。
500ということは、一番近い2のべき乗は512・・・
float型なので・・・512 * 4 = 2kByte

この2kByteという数字に何か意味があるのかな・・・？
応急措置として、プログラムを以下のように書き換えます。

mat_a = (float**)malloc(sizeof(float*) * size);
for(int i = 0; i<size; i++)
    mat_a[i] = (float*)malloc(sizeof(float) * 5230);
    //mat_a[i] = (float*)malloc(sizeof(float) * size);

5230である理由は、行列のサイズが4610の時に性能が良かったので、そこに512を足しただけです。
本当はもっといい方法があるはずなので、真似しないように。
これで処理時間を計測してみます。

f:id:yukirunrun:20200607015149p:plain

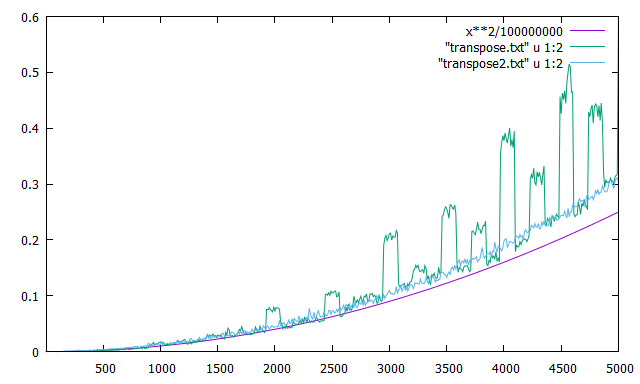
グラフの緑色が変更前、水色が変更後です。
グラフの凹凸がなくなり、二乗曲線のような特性に近づきました。
予想通りといえば予想通りなんだけど、どうしてなんだろうね・・・？

パタヘネを読んでいると、一番関係ありそうなのはTLB（ Translation Lookaside Buffer）です。
いわゆるメモリ仮想化技術における、ページのキャッシュですね。
ただ今回の調査はメモリに対して負荷をかけていないつもりだし、これが原因なのか？
コンピュータに詳しい人、ご意見よろしくお願いします m(._.)m